“管综数学角”是泰祺教育打造的精品学科栏目之一，专注于管理类联考综合卷的数学科目。通过定期发布管综数学的复习攻略、备考规划、难点突破、解题技巧等干货分享，旨在帮助同学们掌握学习方法、提高学习兴趣，为数学备考助一臂之力！
本文作者：吴可一老师
泰祺教育数学教研组老师
函数、方程、不等式是联考中每年必考的内容，一般会考3-4题，它们可以很好地结合其他知识点进行考察，具有一定的灵活性和综合性。
这部分内容在初高中的学习中也是一个重点，但是对综合性的考察要求不是很高，所以很多同学对这部分知识的理解和掌握仅停留在对公式的机械记忆。这种情况会让我们在认知结构中完全把函数、方程、不等式三个部分割开来。而联考解题时间有很强的限制性，所以更需要我们要对这几个知识点深入理解，熟练掌握。
下面我们先以图表的形式，展示一下一元二次函数、一元二次方程、一元二次不等式三个知识点之间的相关性。
上表显示，方程的根和不等式解集的不同情况，都可以在函数的图象上集中体现。那么这些知识点究竟如何考察，如何在解题中加以运用，我们以下列题目为例进行说明。
轴的交点的横坐标，即为对应方程的根，也是不等式解集的端点值，并且能从函数图象直接读出所求不等式的解集。
总结：
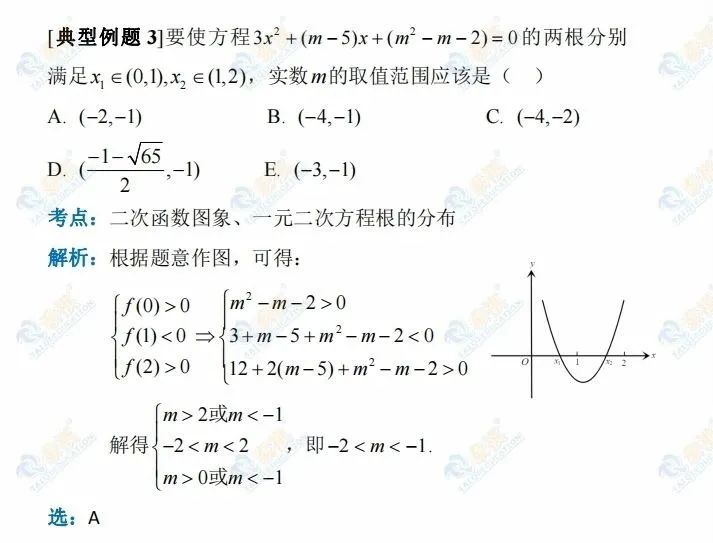
本题用数形结合的思想，结合一元二次函数图象，解决一元二次方程根分布的问题。通过限制根所在区间的端点函数值的正负，使方程的根满足所要求的条件。
除了我们熟悉的一元二次函数以外，联考大纲还涉及到指数函数和对数函数。下面再来看一下指数函数。
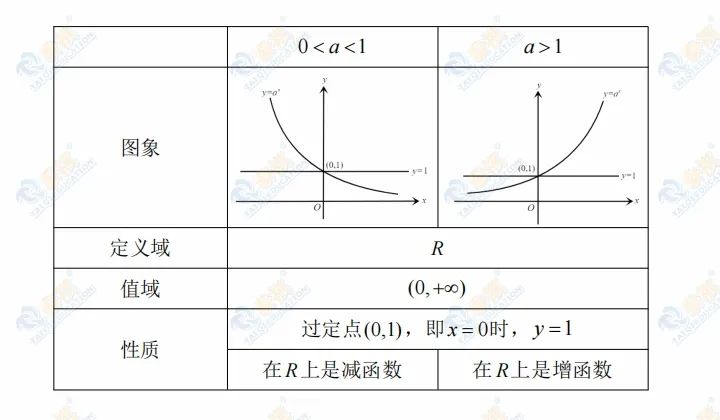
如上表所示：
联考中对于指数函数的考察，基本围绕指数函数单调性的应用。
从历年的真题来看，函数方程不等式在应用题、数列，乃至几何中都有一定的应用。而通常其图象就能直观地体现出所有可能的考点、要点，因此需要在牢记知识点的基础上精准理解，并要在刷题的过程中好好体会。
